To path indicator Subpages of “Events“ To navigation To quick access To footer with other services
To content
Algorithm Engineering
Fakultät für Informatik
Students in summer on north campus, red gears in background. © Roland Baege​/​TU Dortmund

tu.hosts - Guest researcher Michiel Smid

Prof. Michiel Smid from Carleton University, Canada, will visit TU Dortmund University from May 12 to 16, 2025. As part of this visit, he will give two lectures to which everyone is invited:

Research Talk, Monday 12.05., 2pm

(~30min talk + discussions & joint coffee break)

Title: Orientations of omplete Geometric Graphs with Average Oriented-Dilation 1+ϵ

Room: OH12, E.003 or online via zoom

Lecture, Wednesday 14.05., 10am-12

(as part of the master's lecture "Algorithmische Geometrie" by Prof. Buchin)

Title: The Well-Separated Pair Decomposition and its Applications 

Room: OH14, 304

During the rest of the week, Prof. Smid will research the WSPD and its applications on (oriented) spanners together with the Algorithm Engineering working group and selected students.

The Guest

Michiel Smid is a renowned expert in computational geometry, especially in the design and analysis of geometric networks.

Michiel Smid received his master’s degree from Eindhoven University of Technology in the Netherlands and his Ph.D.  from the University of Amsterdam. From 1990 to 1996, he worked as a research associate at the Max-Planck-Institute for Computer Science in Saarbrücken, Germany. Prior to joining Carleton’s faculty, Michiel Smid was a professor of Theoretical Computer Science at the Institute of Simulation and Graphics at the University of Magdeburg, Germany. He joined the School of Computer Science at Carleton University as an Associate Professor in 2001 and has been a full professor with the school since 2004.

The Topic

The Well-Separated Pair Decomposition (WSPD) is a mathematical technique that helps to break down complex arrangements of points in space into simpler, more manageable parts. This method is particularly useful for solving problems efficiently such as nearest-neighbor search (finding the closest object to a given point), clustering (grouping similar objects), and range searching (finding all objects within a specific distance). A key advantage of WSPD is its applicability in both two-dimensional and higher-dimensional spaces, making it  a valuable tool in areas as diverse as geography, network analysis, and machine learning. By reducing the number of calculations, WSPD enables faster data processing, which is essential for handling enormous datasets.

Recommended literature: The well-separated pair decomposition and its applications by Michiel Smid

© Antonia Kalb​/​TU Dortmund
Spanner (black), a subgraph of the complete graph (grey) constructed by WSPD (disks).

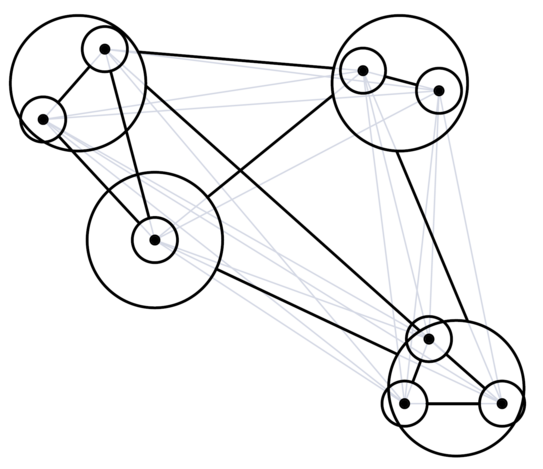
In network analysis, WSPD is used to compute a spanner, a simplified network that retains key properties, particularly the distance between points in the reduced graph.

Since 2024, the computational geometry groups at Carleton University and TU Dortmund  collaborate. For example, we are jointly researching oriented spanners, a specialized type of directed spanners with only one-way edges. By utilizing WSPD, our algorithm to construct oriented spanners achieves efficient construction time and high-quality approximations for multidimensional point sets.

The Programm

tu.hosts enables doctoral researchers to finance guest lectures or workshops of international top researchers.

If you have any questions or require further information, please do not hesitate to reach out: antonia.kalbtu-dortmundde

To top of page